Radx2Grid Gridding Options

Overview

There are several methods available to grid radar data, complete with strengths and weaknesses, which will be described below. Both methods here have lineages back to the 1970's and have been used prolifically in the community. These two methods are sometimes referred to "SPRINT" (Mohr et al. 1979) and "REORDER" (Oye and Case, 1995). RadX2Grid relies on a bilinear interpolation as a default, but can be setup to do a REORDER-type filtering/ smoothing operation.

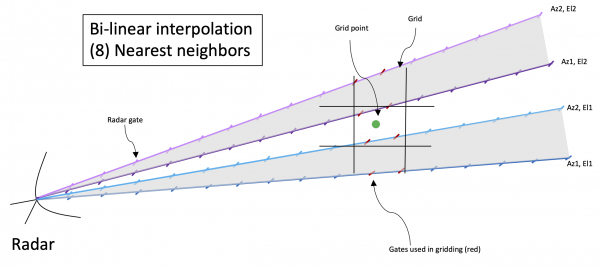
Bilinear Interpolation ('aka' SPRINT)

Bilinear interpolation takes an average of the closest (8) gates (two in azimuth by two in elevation by two in range) to a given grid point. In radar space, this can be thought of as the 2 range gates in front and behind the grid point from the two closest azimuths, and similarly two points from the closest two azimuths from the next elevation angle, as illustrated in the cartoon below.

More information from NCAR: Link

PROS:

• This is a true interpolation scheme, no smoothing.
• It is better at preserving small variations in the data.
• It more naturally captures the sampling resolution in the original radar range-azimuth-elevation sampling domain.

CONS:

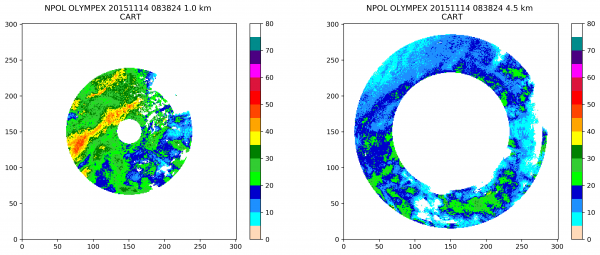
• If there are not enough points nearby for the interpolation, gaps in the data can be large. This can lead to "ringing" in height, and a smaller than expected domain at lower elevations. See figures below.
• If the grid is larger than the azimuthal /elevation stepping (such as close to the radar), some gates may never be used.

This was gridded using this File:Radx2Grid.npol.olympex.cart.txt parameters input file with 0.5 km grid spacing. For this type of gridding it is important to consider the grid spacing and the number of points needed to result in a "valid" grid point.The lower the number of valid points, the more "marginal" points will be included. The relevant parameters in the params file are:

interp_mode = INTERP_MODE_CART;

min_nvalid_for_interp = 4;

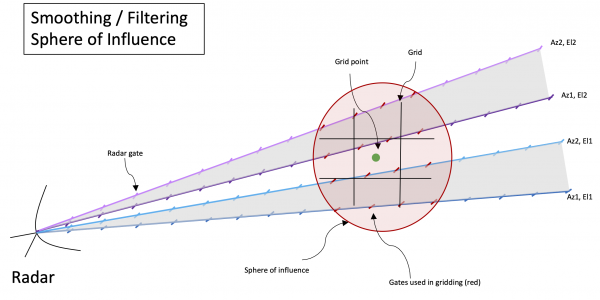
Filtering /Smoothing ('aka' REORDER)

The "REORDER" method is a smoothing / filtering method of gridding radar data. In this case, the user specifies a weighting function (often a Cressman filter) and a "sphere of influence" over which all the radar gates are averaged with the weighting function, as demonstrated in the cartoon below.

More information from NCAR: Link

PROS:

• This can result in a more continuous radar coverage over the domain
• Points are weighted by their distance to the grid point

CONS:

• This is not a true "interpolation" methodology, and smooths the data
• Close to the radar a lot of points are included in the sphere, but far from the radar few or none can be in the sphere of influence, depending on the radar scan strategy and size of sphere of influence. This is somewhat mitigated by letting the size of the influence vary with range from the radar, such as with the reorder_scale_search_radius_with_range =True, in conjunction with the reorder_nominal_range_for_search_radius_km which is the point at which the radius that is set results.
• This also results in "ringed" artifacts

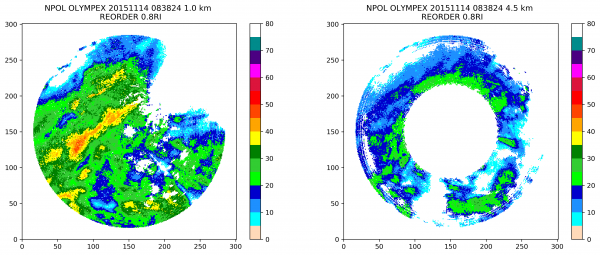
Here is an example using a 0.8 km search radius, and 0.5 km grid spacing:

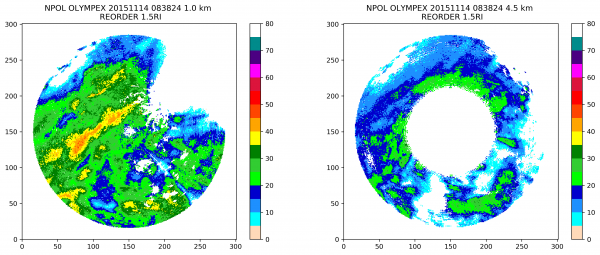
And the same setup but with 1.5 km search radius (note the differences in the intensity of the snow band at 1.0 km, and differences in the edge effects at far ranges at 4.5 km):

These were gridded using this File:Radx2Grid.npol.olympex.reorder1.5.txt parameters input file with 0.5 km grid spacing and either 1.5 or 0.8 km for the reorder_search_radius_km. For this type of gridding, the search radius is critical and will have a large impact on the resulting grid, s seen above. A starting place is to have a ROI approximately similar to the grid spacing. The relevant parameters in the params file are:

interp_mode = INTERP_MODE_CART_REORDER;

reorder_npoints_search = 24;

reorder_search_radius_km = 1.5;

reorder_scale_search_radius_with_range = TRUE;

reorder_nominal_range_for_search_radius_km = 60;

reorder_z_search_ratio = 1.0;

reorder_only_use_one_point_per_octant = FALSE;

reorder_bound_grid_point_vertically = FALSE;

reorder_min_valid_wt_ratio = 0.5;

reorder_blocks_nrows = 8;

reorder_blocks_ncols = 8;

References

Mohr, C. G., and R. L. Vaughan, 1979: An economical procedure for Cartesian interpolation and display of reflectivity factor data in three-dimensional space. J. Appl. Meteor.,18, 661–670. Link

Oye, D., and M Case, 1995: REORDER: A program for gridding radar data. User's Manual. National Center for Atmospheric Research. Link