RadxRate equations

Overview

The goal of RadxRate is to estimate the precipitation rate at each gate within a three-dimensional radar volume. RadxRate includes several equations for estimating precipitation rate, which can be tuned according to the specific environment and precipitation type. This page will walk through these equations.

Polarimetric-based estimates

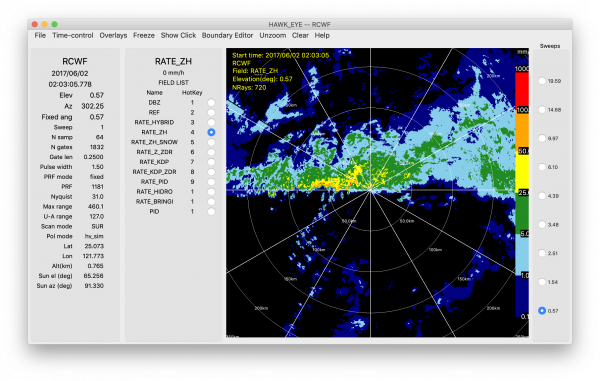
R(Z)

Probably the most straightforward method of estimating precipitation rates, precipitation (mostly rainfall) can be estimated using an equation in the following form:

Many variations of this equation exist, depending on the precipitation conditions (e.g., convective vs stratiform, tropical vs midlatitude). An example of the estimated precipitation using a tropical version of this equation from northern Taiwan is shown in the image below. Since this particular example is from the lowest elevation angle, the echoes within ~150 km should all correspond to rain. Coefficients for Z-R relationships have been developed for dry snow, but aren't shown here given the warm environment near Taiwan.

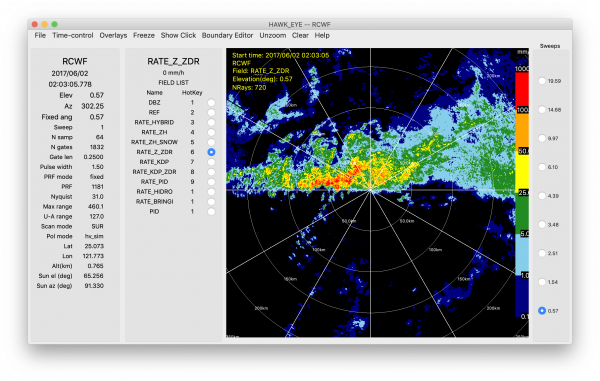
R(Z, ZDR)

Z-R relationships are known to be overly simplistic, as reflectivity depends on both hydrometeor size and concentration and single polarization only captures hydrometeor size in one dimension. Relationships that take both Z and ZDR, and thus the shape of particles, into account have been developed, which take the form:

An example of the estimated precipitation using coefficients from Berkowitz et al. (2013) is shown below.

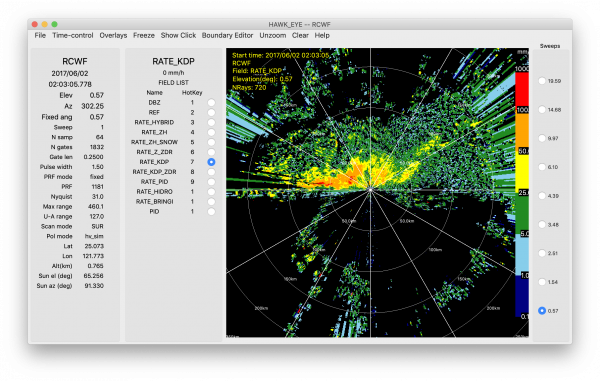
R(KDP)

KDP has also been used to estimate precipitation rates due to its relationship to the rain water content that slows down the propagating wave. RadxRate enables the use of KDP in precipitation rate estimation using the following form:

An example of the estimated precipitation using coefficients from Berkowitz et al. (2013) is shown below.

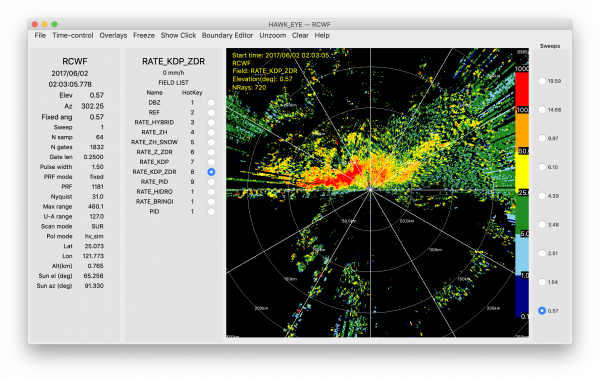
R(KDP, ZDR)

PID-based estimates

In addition to the aforementioned relationships that estimate precipitation rates directly from polarimetric variables, RadxRate includes relationships that prescribe different relationships based on the dominant hydrometeor type inferred from the polarimetric radar data. That is, these PID-based algorithms will apply different equations to gates dominated by large raindrops and dry snow. All require the PID algorithm to be applied to the radar volume, which is done in an earlier step of RadxRate.

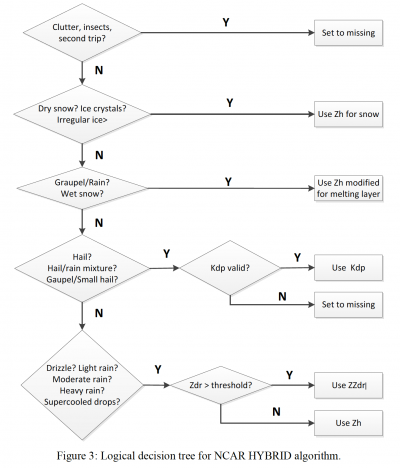
NCAR Hybrid

The NCAR Hybrid method applies some of the aforementioned precipitation rate equations to different PID categories. The method is described in the logical decision tree below (Dixon et al. 2015).

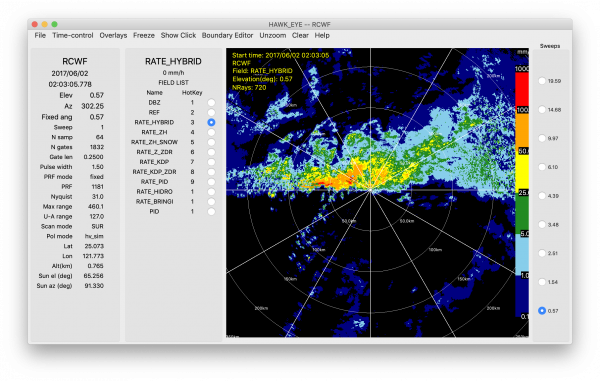
An example of the NCAR hybrid method is shown below.

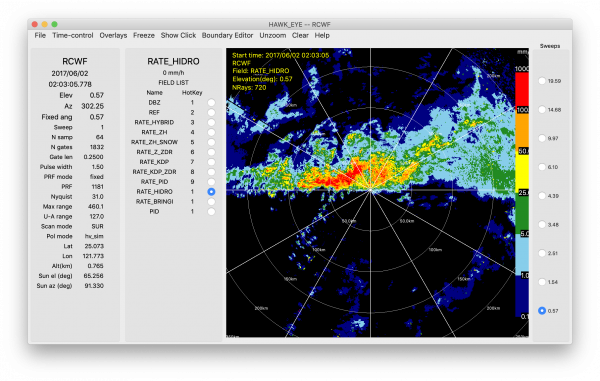
CSU HIDRO

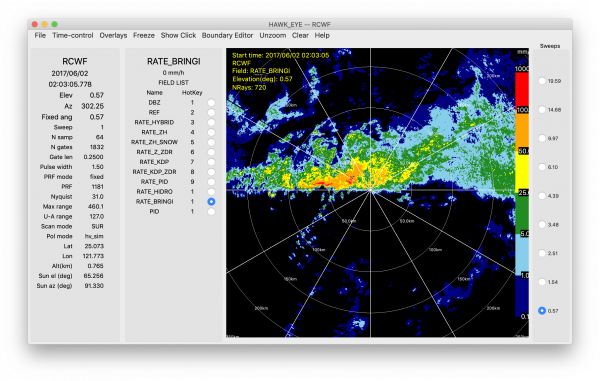
Bringi

References

Berkowitz, D. S., J. A Schultz, S. Vasiloff, K.L. Elmore, C.D. Payne and J.B. Boettcher, 2013: Status of Dual Pol QPE in the WSR-88D Network. AMS 27th conference on hydrology, Austin, Texas, 2.2. Link

Bringi, V. N., Williams, C. R., Thurai, M., & May, P. T. (2009). Using Dual-Polarized Radar and Dual-Frequency Profiler for DSD Characterization: A Case Study from Darwin, Australia, Journal of Atmospheric and Oceanic Technology, 26(10), 2107-2122. Link

Cifelli, R., Chandrasekar, V., Lim, S., Kennedy, P. C., Wang, Y., & Rutledge, S. A. (2011). A New Dual-Polarization Radar Rainfall Algorithm: Application in Colorado Precipitation Events, Journal of Atmospheric and Oceanic Technology, 28(3), 352-364. Link

Dixon, M. J., J. W. Wilson, T. M. Weckwerth, D. Albo, and E. J. Thompson, 2015: A dual-polarization QPE method based on the NCAR particle ID algorithm: Description and preliminary results. 37th Conf. on Radar Meteorology, Norman, OK, Amer. Meteor. Soc., 9A.1. Link