Difference between revisions of "RadxPid fuzzylogic"
From Lrose Wiki
| Line 15: | Line 15: | ||
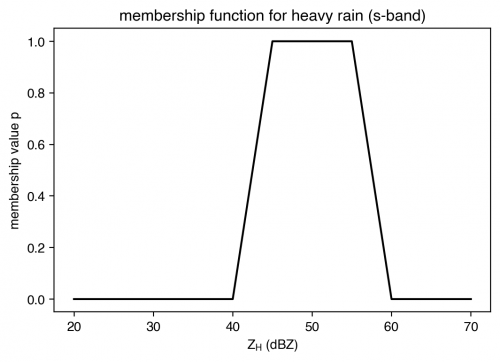
| − | The single-variable membership functions are described in lines 106-123. The first column describes the polarimetric variable (<math>Z_H</math>) and the PID category, the second column describes the full range of <math>Z_H</math> values considered, and the remaining columns describe the membership function shape. An example of the <math>Z_H</math> membership function for Heavy Rain is shown in the image below. Below 40 dBZ (column 3) and above 60 dBZ (column 6) the membership value is 0, between 45 and 55 dBZ (columns 4 and 5) the membership value is 1, and | + | The single-variable membership functions are described in lines 106-123. The first column describes the polarimetric variable (<math>Z_H</math>) and the PID category, the second column describes the full range of <math>Z_H</math> values considered, and the remaining columns describe the membership function shape. An example of the <math>Z_H</math> membership function for Heavy Rain is shown in the image below. Below 40 dBZ (column 3) and above 60 dBZ (column 6) the membership value is 0, between 45 and 55 dBZ (columns 4 and 5) the membership value is 1, and between 40-45 dBZ and 55-60 dBZ the membership function transitions linearly. Categories with only 3 columns either indicate that the membership value remains 1 at the end of the full <math>Z_H</math> range or that the decrease to 0 occurs linearly to end of the range. |
[[File:Hr_zh_sband_memfunc.png|500px]] | [[File:Hr_zh_sband_memfunc.png|500px]] | ||
Revision as of 20:55, 5 February 2021
Overview
RadxPid uses polarimetric radar data to provide a best estimate of the dominant particle type at every radar gate. The categorization is done by using a fuzzy logic algorithm, which describes the likelihood that different values of polarimetric variables are caused by different particles. RadxPid uses the method described by Vivekanadan et al. (1999) and this page will highlight the most important concepts in the algorithm.
Fuzzy Logic Basics
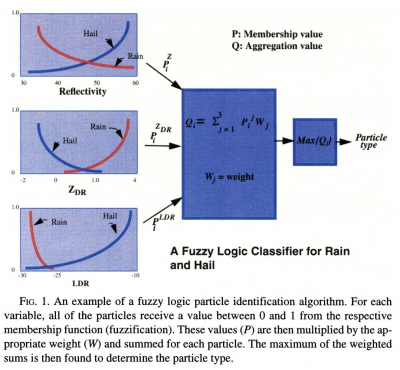
As described in Vivekanadan et al. (1999), fuzzy logic methods are similar to probabilistic methods in that they describe uncertainty on a scale from 0 to 1, except fuzzy logic categories do not have hard boundaries. For example, radar gates that have rain or hail can have similar reflectivity values, although rain is more likely to have certain reflectivity values than hail. The fuzzy logic method assigns a likelihood (i.e., a membership value p) that rain or hail is associated with a particular reflectivity value defined by a membership function as shown in the image below. Membership functions can be created for a single polarimetric variable and combinations of polarimetric variables. Thus, membership functions are applied to the polarimetric data at each gate, providing a membership value (from 0 to 1) for each particle type and polarimetric variable/combination. Each membership value is then multiplied by a predetermined weight, the weighted values from each polarimetric variable/combination are summed, producing an aggregation value for each particle category. The particle type that has the largest aggregation value is then the dominant particle type at that gate and is assigned a particular PID value at that gate.
Fuzzy Logic in RadxPid
The membership functions and weights are all set in the PID thresholds file. Due to variations in the polarimetric responses of particles to radar characteristics, different files are required (e.g., S- vs X-band, simultaneous vs alternating transmission). The following examples will all assume a simultaneously transmitting S-band radar (e.g., WSR-88D).
18 PID categories are possible, including categories like heavy rain to hail to insects (lines 14-31). Weights for each variable are assigned on line 63 and include temperature, [math]\displaystyle{ Z_H }[/math], [math]\displaystyle{ Z_{DR} }[/math], [math]\displaystyle{ K_{DP} }[/math], [math]\displaystyle{ LDR }[/math], [math]\displaystyle{ \rho_{HV} }[/math], [math]\displaystyle{ \sigma(Z_{DR}) }[/math], and [math]\displaystyle{ \sigma(\phi_{DP}) }[/math]. Some absolute thresholds are included in lines 67-95. For example, any gates where [math]\displaystyle{ Z_{DR} \lt = 0 }[/math] will return a membership value of 0 for Heavy Rain (line 81).
The single-variable membership functions are described in lines 106-123. The first column describes the polarimetric variable ([math]\displaystyle{ Z_H }[/math]) and the PID category, the second column describes the full range of [math]\displaystyle{ Z_H }[/math] values considered, and the remaining columns describe the membership function shape. An example of the [math]\displaystyle{ Z_H }[/math] membership function for Heavy Rain is shown in the image below. Below 40 dBZ (column 3) and above 60 dBZ (column 6) the membership value is 0, between 45 and 55 dBZ (columns 4 and 5) the membership value is 1, and between 40-45 dBZ and 55-60 dBZ the membership function transitions linearly. Categories with only 3 columns either indicate that the membership value remains 1 at the end of the full [math]\displaystyle{ Z_H }[/math] range or that the decrease to 0 occurs linearly to end of the range.
Example
References
Vivekanandan, J., Zrnic, D. S., Ellis, S. M., Oye, R., Ryzhkov, A. V., & Straka, J. (1999). Cloud Microphysics Retrieval Using S-Band Dual-Polarization Radar Measurements, Bulletin of the American Meteorological Society, 80(3), 381-388. Link